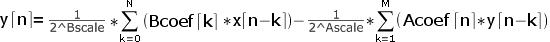This function applies IIR filter to ptrInput.

• BScale: B scale factor.
• AScale: A scale factor.
• ptrB: pointer to B coefficients (in program memory).
• ptrA: pointer to A coefficients (in program memory).
• FilterOrder: order of the filter + 1.
• ptrInput: address of input samples.
• InputLen: number of samples.
• ptrOutput: pointer to output samples. Output length is equal to Input length.
• Index: index of current sample.

Function returns value of the Index-th sample of the filtered signal :

Nothing.

// Filter setup:
//     Filter kind: IIR
//     Filter type: Lowpass filter
//     Filter order: 2
//     Design method: Butterworth

program IIR;


const FILTER_ORDER : word = 2;
      COEFF_B : array[FILTER_ORDER+1] of integer = (0x344D, 0x689A, 0x344D);
      COEFF_A : array[FILTER_ORDER+1] of integer = (0x4000, integer(0xA003), 0x2687);
      SCALE_B : integer =  4;
      SCALE_A : integer =  -1;
var
     inputSamples : array[3] of integer;
     outputSamples : array[10] of integer;
     i             : word;

procedure Init();
  begin
  inputSamples[0] := 0x4000;
  inputSamples[1] := 0x2000;
  inputSamples[2] := 0x1000;
  end;

begin
  Init();
  for i := 0 to 6 do
   outputSamples[i] := IIR_Radix(SCALE_B, SCALE_A, @COEFF_B, @COEFF_A, FILTER_ORDER+1, @inputSamples, 3, @outputSamples, i);
   // outputSamples[0] = 1/(2^SCALE_B)*COEFF_B[0]*inputSamples[0]
   // outputSamples[1] = 1/(2^SCALE_B) * (COEFF_B[0]*inputSamples[1] + COEFF_B[1]*inputSamples[0]) - 1/(2^SCALE_A)*(COEFF_A*outputSamples[0])
   // .
   // .
   // .
end.

None.