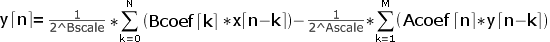IIR Filter Library
  mikroBasic PRO for PIC32 Libraries > DSP Libraries > 
  

IIR Filter Library

mikroBasic PRO for PIC32 includes a library for Infinite Impulse Response (IIR) filter. All routines work with fractional Q15 format.

A infinite impulse response (IIR) filter is a type of a digital filter, whose impulse response (the filter's response to a delta function) is non-zero over an infinite length of time.

Library Routines

IIR_Radix

Prototype

sub function IIR_Radix(dim const BScale as integer, dim const AScale as integer, dim ptrB as ^const integer, dim ptrA as ^const integer, dim FilterOrder as word, dim ptrInput as ^integer, dim InputLength as word, dim ptrOutput as ^integer, dim Index as word) as integer
Description

This function applies IIR filter to ptrInput.
Parameters
  • BScale: B scale factor.
  • AScale: A scale factor.
  • ptrB: pointer to B coefficients (in program memory).
  • ptrA: pointer to A coefficients (in program memory).
  • FilterOrder: order of the filter + 1.
  • ptrInput: address of input samples.
  • InputLen: number of samples.
  • ptrOutput: pointer to output samples. Output length is equal to Input length.
  • Index: index of current sample.
Returns

Function returns value of the Index-th sample of the filtered signal :
Requires

Nothing.
Example 
' Filter setup:
'     Filter kind: IIR
'     Filter type: Lowpass filter
'     Filter order: 2
'     Design method: Butterworth

program IIR


const FILTER_ORDER as word = 2
      COEFF_B as integer[FILTER_ORDER+1] = (0x344D, 0x689A, 0x344D)
      COEFF_A as integer[FILTER_ORDER+1] = (0x4000, integer(0xA003), 0x2687)
      SCALE_B as integer =  4
      SCALE_A as integer =  -1
dim
     inputSamples  as integer[3]
     outputSamples as integer[10]
     i             as word

sub procedure Init()
  inputSamples[0] = 0x4000
  inputSamples[1] = 0x2000
  inputSamples[2] = 0x1000
  end sub

main:
  Init()
  for i = 0 to 9
   outputSamples[i] = IIR_Radix(SCALE_B, SCALE_A, @COEFF_B, @COEFF_A, FILTER_ORDER+1, @inputSamples, 3, @outputSamples, i)
  next i
  asm nop end asm
   ' outputSamples[0] = 1/(2^SCALE_B)*COEFF_B[0]*inputSamples[0]
   ' outputSamples[1] = 1/(2^SCALE_B) * (COEFF_B[0]*inputSamples[1] + COEFF_B[1]*inputSamples[0]) - 1/(2^SCALE_A)*(COEFF_A*outputSamples[0])

end.
Notes

None.
Copyright (c) 2002-2012 mikroElektronika. All rights reserved.
What do you think about this topic ? Send us feedback!
Want more examples and libraries? 
Find them on LibStock - A place for the code